Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности,
| → |
| n |
— фиксированный вектор.
Обозначим j = j(M) — угол между векторами AB и
| → |
| n |
(рис. 1).
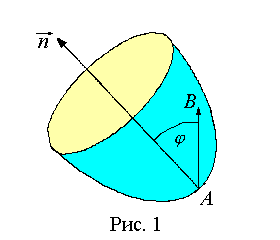
Ненулевой вектор
| → |
| n |
называется нормальным вектором к поверхности в точке A, если
|
Точка поверхности F(x,y,z) = 0 называется обыкновенной, если в этой точке
- частные производные F‘x , F‘y , F‘z непрерывны;
- (F‘x)2 + (F‘y)2 + (F‘z)2 ≠ 0 .
При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности.
Теорема 1. Если M(x0, y0, z0) — обыкновенная точка поверхности F(x,y,z) = 0 , то вектор
|
(1) |
является нормальным к этой поверхности в точке M(x0, y0, z0) .
Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова «Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения». М.: Изд–во МЭИ, 2002 (стр. 128).
Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.
Канонические уравнения нормали можно представить в виде
|
(2) |
Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.
Из этого определения следует, что уравнение касательной плоскости имеет вид:
|
(3) |
Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.
Геометрический смысл полного дифференциала функции двух переменных
Пусть функция z = f(x, y) дифференцируема в точке a(x0, y0) . Ее графиком является поверхность
f(x,y) − z = 0.
Положим z0 = f(x0, y0) . Тогда точка A(x0, y0, z0) принадлежит поверхности.
Частные производные функции F(x, y, z) = f(x, y) − z суть
F‘x = f‘x, F‘y = f‘y, F‘z = − 1
и в точке A(x0, y0, z0)
- они непрерывны;
- F‘2x + F‘2y + F‘2z = f‘2x + f‘2y + 1 ≠ 0 .
Следовательно, A — обыкновенная точка поверхности F(x, y, z) и в этой точке существует касательная плоскость к поверхности. Согласно (3), уравнение касательной плоскости имеет вид:
f‘x(x0, y0) (x − x0) + f‘y(x0, y0) (y − y0) − (z − z0) = 0.
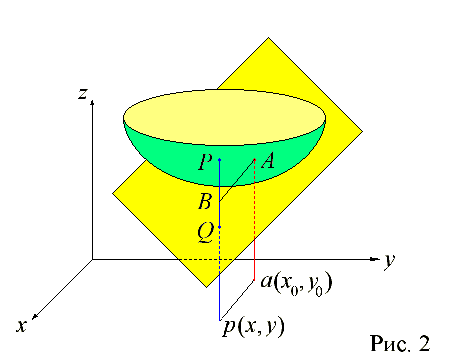
Вертикальное смещение точки на касательной плоскости при переходе из точки a(x0, y0) в произвольную точку p(x, y) есть BQ (рис. 2). Соответствующее приращение аппликаты есть
(z − z0) = f‘x(x0, y0) (x − x0) + f‘y(x0, y0) (y − y0)
Здесь в правой части стоит дифференциал dz функции z = f(x,y) в точке a(x0, x0). Следовательно,
df(x0, y0). есть приращение аппликаты точки плоскости касательной к графику функции f(x, y) в точке (x0, y0, z0 = f(x0, y0)).
Из определения дифференциала следует, что расстояние между точкой P на графике функции и точкой Q на касательной плоскости есть бесконечно малая более высокого порядка, чем расстояние от точки p до точки a.
