Пусть заданы функция u = u(x1, x2, … , xn) = u(x) , определенная в некоторой окрестности точки
a(a1, a2, … , an) О Rn , и l — единичный вектор ( || l || = 1 ).
Через точку a проведем прямую в направлении вектора l и обозначим символом
Δl u = u(x) − u(a) приращение функции, которое она получает при смещении из точки a в некоторую точку x на этой прямой. Обозначим символом Δl величину смещения, т.е.
|
(см. Рис. 1).
Производной функции u(x) в точке a по направлению l называется предел отношения Δl u к Δl при Δl → 0.
Обозначение
|
(1) |
Производная по направлению характеризует скорость изменения функции в данной точке в данном направлении.
Выведем формулу для производной по направлению. Для этого используем параметрические уравнения прямой
|
где x = (x1, x2, … , xn) , a = (a1, a2, … , an ) и l — единичный направляющий вектор прямой. Переменная t имеет тот же смысл, что и Δl.
Сужение функции u = u(x) на данную прямую есть функция f(t) одной переменной t:
|
, причем f(0) = u(a). Тогда из определения (1) следует, что
|
(2) |
В частном случае трехмерного пространства u = u(x, y, z) ,
| → |
| l |
= {cosα, cosβ,cosγ}, где α, β, γ — углы, образованные вектором
| → |
| l |
с осями координат. Параметрические уравнения прямой имеют вид
|
Находим ∂u/∂l в точке a по формуле (2). Для этого дифференцируем
f(t) = u(a1 + t · cosα, a2 + t · cos β, a3 + t · cos γ)
как сложную функцию t при t = 0. Получаем
|
Аналогично производная функции u = u(x1, x2, … , xn) в точке a = (a1, a2, … , an) в направлении единичного вектора l = {l1, l2, … , ln} ( l12 + l22 + … + ln2 = 1 ) вычисляется по формуле
|
Геометрический смысл производной по направлению функции двух переменных
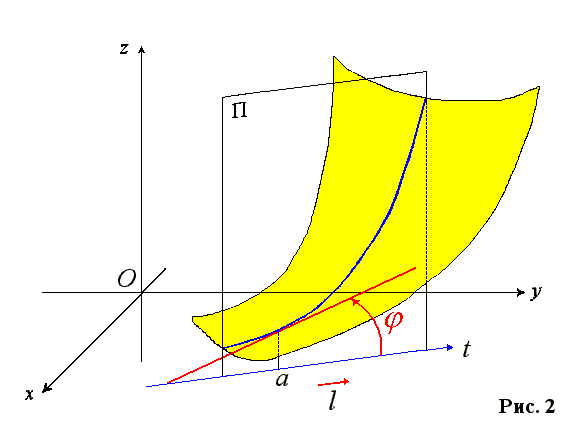График функции z = u(x, y) представлен на рис. 2 поверхностью желтого цвета. Пусть даны точка a и единичный вектор l. Поясним геометрический смысл производной функции u в точке a по направлению вектора l.
Проведем числовую ось через точку a параллельно вектору l. Начало отсчета на этой оси выберем в точке a. Положение любой точки на оси определяется числом t.
Проведем плоскость П через ось at параллельно оси Oz. Плоскость П пересекает график функции z = u(x, y) по кривой, изображенной на рис. 2 синим цветом. Эта кривая является графиком сужения функции z = u(x, y) на прямую a + l·t, т.е. графиком функции f(t) = u(ax+lx·t, ay+ly·t)
Касательная к графику функции f(t) (синей кривой) в точке (0, f(0)) изображена на рис. 2 красным цветом. Она образует с положительной частью оси at некоторый угол φ. Имеем
|
