1. Площадь криволинейной трапеции.
Пусть функция f(x) непрерывна на отрезке [a, b ] и неотрицательна, т.е. f(x) ≥ 0 при всех x О [ a, b]. Рассмотрим фигуру, ограниченную графиком функции y = f(x ) и прямыми x = a, x = b,
y = 0 (рис. 1).
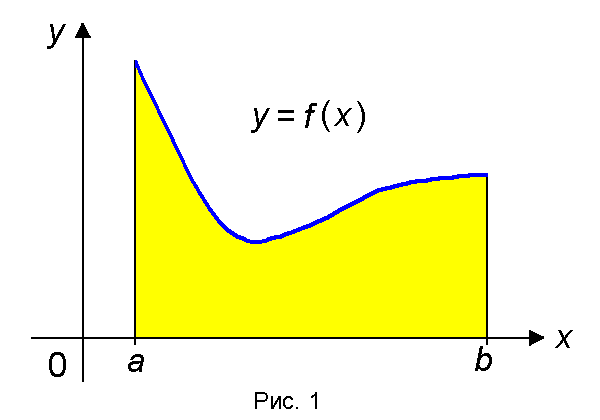
Такую фигуру называют криволинейной трапецией.
Наша задача — дать определение и указать способ вычисления площади криволинейной трапеции. Для этого произвольно разобьем отрезок [a, b ] на n отрезков точками
| x0 = a < x1 … < xk − 1 < xk < … < xn − 1 < xn = b. | (1) |
Проведем через эти точки прямые, параллельные оси OY.
Тогда криволинейная трапеция разобьется на n частей, каждая из которых является криволинейной трапецией.
Введем обозначения
Δxk = xk − xk − 1 (k = 1,…,n); λ =
Δxk. |
(2) |
На каждом отрезке [x k − 1, x k ] выберем произвольным образом точку ξk (k = 1, …,n).
Рассмотрим фигуру, состоящую из прямоугольников с основаниями Δxk и высотами f(ξk). (рис. 2)
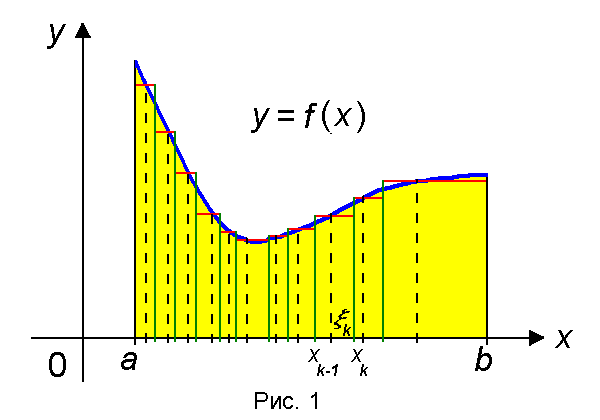
Площадь Sn этой фигуры вычисляется по формуле
Sn =
. |
Очевидно, что при достаточно малых отрезках Δxk эта фигура будет мало отличаться от исходной криволинейной трапеции. Поэтому за площадь S криволинейной трапеции естественно принять предел площадей таких фигур при стремлении к нулю длин всех отрезков разбиения
S =
Sn =
|
(3) |
(при условии, что указанный предел существует и не зависит ни от способа разбиения отрезка [a, b] на части, ни от выбора точек ξk).
2. Понятие определенного интеграла
Пусть функция f(x) определена на отрезке [a, b]. Разобьем отрезок [a, b ] на n отрезков точками
| x0 = a < x1 < … < xk − 1 < xk < … < xn − 1 < xn = b |
и введем обозначения
Δxk = xk − xk − 1 (k = 1, …,n); λ =
Δxk. |
На каждом отрезке [x k − 1, x k] выберем произвольным образом точку ξk (k = 1, …,n) и составим сумму
f(ξk) · Δxk , |
(5) |
называемую (римановой) интегральной суммой функции f(x) на отрезке [a, b ].
Если существует конечный предел интегральных сумм (5) при λ → 0, причем этот предел не зависит ни от способа разбиения отрезка [a , b] на части, ни от выбора точек ξk, то функция f(x) называется интегрируемой (по Риману) на отрезке [a, b ], а указанный предел называется (римановым) определенным интегралом от f(x) по отрезку [a, b ] и обозначается символом
f(x) dx . |
Таким образом,
f(x) dx =
f(ξk) · Δxk . |
Замечание. Данное Риманом определение интеграла оказалось неудачным. Современная терия интегрирования опирается на определение, данное Лебегом. Она гораздо более мощная и простая в применениях, чем теория Ремана.
3. Необходимое условие интегрируемости
Теорема 1. Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.
Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики : Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М. : Изд–во МЭИ, 2002. (Стр. 41.)
Замечание. Ограниченность функции не является достаточным условием ее интегрируемости.
Достаточные условия интегрируемости
Теорема 2. Если выполнено одно из следующих условий :
- функция f(x) непрерывна на отрезке [a, b ];
- функция f(x) ограничена на отрезке [a, b] и имеет на этом отрезке конечное число точек разрыва;
- функция f(x) монотонна на отрезке [a, b],
то f(x) интегрируема на отрезке [a, b] и, следовательно,
f(x) dx |
существует.
4. Геометрический смысл определенного интеграла
Из теоремы 2 и формулы (3) следует, что если функция f(x) непрерывна и неотрицательна на отрезке [a, b], то площадь S криволинейной трапеции, ограниченной графиком функции y = f(x) и прямыми x = a, x = b, y = 0 (рис. 1), вычисляется по формуле
S =
f(x) dx . |
