Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.
Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.
Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)
Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].
Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что «x О [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b] (рис.2).
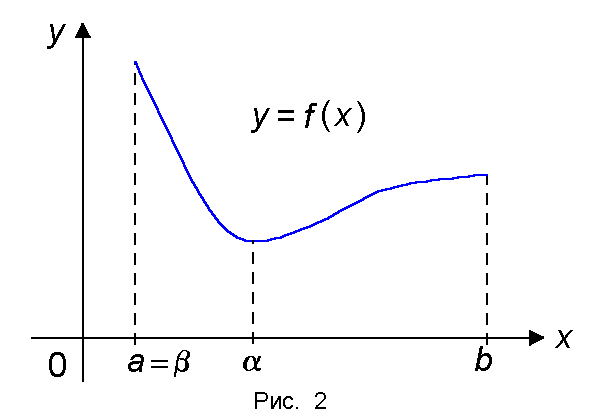
Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
Замечание. На этой теореме основан метод приближенного решения уравнения
| f(x) = 0, | (1) |
называемый методом бисекции (дихотомии), или методом половинного деления.
Схема решения уравнения методом половинного деления
- Отделяем корни уравнения (1). Для этого устанавливаем промежутки, в которых функция f(x) имеет единственный нуль и на его концах принимает значения разных знаков. С этой целью используем графические построения или составляем таблицу значений функции. Обозначим такой отрезок символом σ0.
- Разделим этот отрезок пополам. Если в середине отрезка функция f(x) равна нулю, уравнение (1) решено. В противном случае на концах одного из полученных половинных отрезков f(x) вновь принимает значения разных знаков. Обозначим этот отрезок символом σ1 и вновь разделим его пополам. Если в середине σ1 функция f(x) равна нулю, то уравнение (1) решено. В противном случае продолжим указанную процедуру. Таким образом, мы либо на каком–то этапе получим точку, в которой f(x) = 0, т.е. точное решение уравнения (1), либо получим последовательность вложенных друг в друга отрезков σ0 Й σ1 Й … , на каждом из которых f(x) имеет значения разных знаков. В этом случае можно заключить искомый корень уравнения (1) в промежуток произвольной длины и, следовательно, вычислить этот корень с любой заданной точностью.
Замечание. Метод неприменим для отыскания корней четной кратности.
Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).
Доказательства теорем приведены в книге Л.Д. Кудрявцева “Краткий курс математического анализа”. Т.1. М.: ФИЗМАТЛИТ, 2002. Стр.122–124.
Cуществование непрерывной обратной функции
Пусть функция y = f(x) определена, строго монотонна и непрерывна на отрезке [a,b]. Тогда на отрезке [α, β] ( α = f(a), β = f(b) ) cуществует обратная функция x = g(y), также строго монотонная и непрерывная на отрезке (α, β).
