Пусть функция y = f(x) определена в некоторой окрестности точки x0.
Функция f(x) называется дифференцируемой в точке х0, если ее приращение представимо в виде
| Δf = f(x0 + Δx) − f(x0) = A · Δx + o(Δx) , |
где A — число, не зависящее от Δх, а o(Δx) — функция более высокого порядка малости чем Δx при Δх → 0 .
Таким образом, приращение дифференцируемой функции является суммой линейной относительно Δx ч асти A · Δx и бесконечно малой более высокого порядка малости чем Δx при Δх → 0.
Линейная часть приращения дифференцируемой функции называется дифференциалом в точке х0 и обозначается символом df(x0), т.е.
| df(x0) = A · Δx. |
Необходимое и достаточное условие дифференцируемости
Теорема 0.1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. При этом
Δf = f‘(x0) · Δx + o(Δx) ,
= 0. |
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 96.
Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е.
| dx ≡ Δx. |
Отсюда следует формула для вычисления дифференциала
| df(x0) = f‘(x0) dx. |
Геометрический смысл дифференциала
Пусть функция f(x) дифференцируема в точке х0. Проведем касательную к графику этой функции в точке M0(x0, f(x0)) (рис. 1).
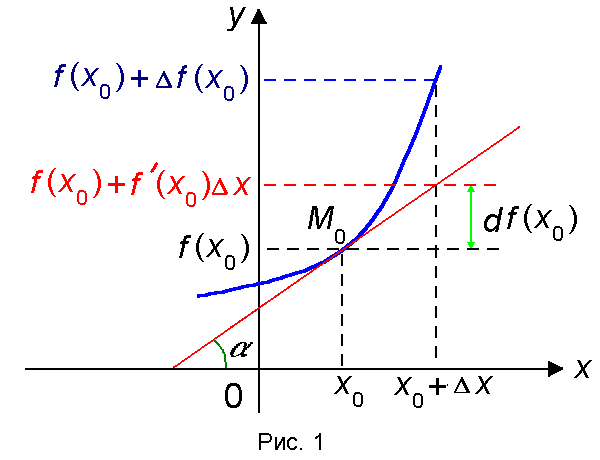
Угловой коэффициент касательной равен tg α = f ‘(x0), где α — угол между касательной и осью OX. При изменении абсциссы х0 на Δx приращение ординаты соответствующей точки касательной равно
| Δx · tg α = f ‘(x0) · Δx ≡ df(x0). |
Таким образом, дифференциал функции f(x) в точке х0 равен приращению, которое получает линейная функция, графиком которой является касательная, при переходе из точки x0 в точку
x0 + Δx.
Применение дифференциала в приближенных вычислениях
Из формулы (1) следует, что при |Δx| << 1 можно пренебречь слагаемым o(x) и тогда
| f(x0 + Δx) ≈ f(x0) + df(x0) = f(x0) + f ‘(x0) · Δx. |
